Deterministik und Probabilistik bei der Sicherheitsbeurteilung technischer Anlagen
(Auszug aus: Probabilistische Risiko- und Sicherheitsanalysen und ihre Anwendungsbereiche,
in: G. Kreysa, O.-U. Langer und N. Pfeil, Quantitative Risikoanalyse – Quo vadis?
Praxis der Sicherheitstechnik, Vol. 7, DECHEMA, Frankfurt a. M. 2006)
Die Auslegung technischer Anlagen erfolgt im Allgemeinen deterministisch. Dabei werden
Beschaffenheitsanforderungen an die benötigten Komponenten, Aggregate usw. vorgeben
und entsprechende Rechnungen durchgeführt. Aus ihnen wird, unter Berücksichtigung
von Sicherheitsfaktoren, deren Dimensionierung abgeleitet.
Diese Vorgehensweise entspringt einem Denken, das charakteristisch ist für die klassische
Physik. Es beinhaltet, dass der Zustand eines Systems zu einer bestimmten Zeit den
Zustand zu einer späteren Zeit (bei fester Umwelt) eindeutig determiniert /1/.
Ein solches Verhalten wird im Allgemeinen durch lineare Differentialgleichungen beschrieben.
Dies ist im Makroskopischen generell möglich, gilt aber bekanntermassen nicht im
Bereich der Quantenphysik (vgl. /1/). Ihre Modelle beruhen auf Wahrscheinlichkeiten,
sind also probabilistisch.
Der Weg von der Deterministik zur Probabilistik bei technischen Fragestellungen soll
nachfolgend an einem beispielhaften Gedankenexperiment verdeutlicht werden.
Wird eine Kugel in eine bestimmte Richtung geworfen, so lässt sich der Punkt ihrer
Landung vorhersagen, wenn
- Flugrichtung und
- Anfangsgeschwindigkeit
vorgegeben sind und der Einfluss des Luftwiderstandes (wegen ihrer stromlinienförmigen
Geometrie) vernachlässigt werden darf. D.h. durch die Anfangsbedingungen ist die
Flugbahn eindeutig festgelegt (determiniert). Wäre diese Kugel nun ein Bruchstück
aus einem Explosionsprozeß, so wäre es schwierig, wenn nicht gar unmöglich, Flugrichtung
und Anfangsgeschwindigkeit vorherzusagen. Infolgedessen würde die Berechnung der
weiteren Flugbahn unmöglich.
Aus Beobachtungen der Vergangenheit könnte aber bekannt sein, welche Flugrichtung
und Anfangsgeschwindigkeit im Mittel zu erwarten sind. Ihre Verwendung erlaubte es
dann, eine mittlere Flugbahn zu berechnen. Die Tatsache, dass Mittelwerte angegeben
werden, deutet darauf hin, dass es sich um Zufallsvariablen (stochastische Variablen)
handelt, d.h. um Größen, die bestimmte Werte mit bestimmten Wahrscheinlichkeiten
annehmen. Solche Variable werden üblicherweise durch Wahrscheinlichkeitsverteilungen
(vgl. /2/) beschrieben. Die Mittelwertbildung stellt somit eine Reduzierung der Information
dar, die in der Wahrscheinlichkeitsverteilung enthalten ist. Würde man die Wahrscheinlichkeitsverteilungen
von Flugrichtung und Anfangsgeschwindigkeit bei den Rechnungen berücksichtigen, so
hätte man es mit einer deterministischen Rechnung mit stochastischen Anfangsbedingungen
zu tun. Statt eines Punktes der Landung, ergäbe sich dann allerdings eine Wahrscheinlichkeitsverteilung
für die Landepunkte, mithin ein probabilistisches Ergebnis (vgl. /3/). An einem Beispiel
wird dies im Bild 1 dargestellt.
Die Wahrscheinlichkeitsverteilung F(x) (Ordinate) gibt an, mit welcher Wahrscheinlichkeit
die Reichweite kleiner oder gleich dem zugehörigen Abszissenwert ist. Man sieht,
dass Flugweiten, die größer sind als der Mittelwert von 40,8 m, auftreten können.
Bei Verwendung des Mittelwertes käme es also zu einer Unterschätzung, was im Zusammenhang
mit Sicherheitsuntersuchungen als „nicht konservativ“ bezeichnet würde.
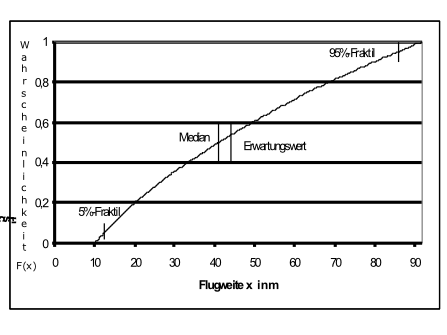
Bild 1: Wahrscheinlichkeitsverteilung F(x) für Flugweiten (Anfangsgeschwindigkeit
v0 gleichverteilt zwischen 10 m/s und 30 m/s, Abflugwinkel gleichverteilt zwischen
0° und 90°, die Flugweite bei Benutzung der entsprechenden Mittelwerten (20 m/s,
45°) beträgt die (maximale) Flugweite 40,8 m)
Legte man andererseits die maximale Geschwindigkeit von 30 m/s zugrunde, so wäre
man übermässig konservativ; es ergäbe sich nämlich eine maximale Weite von 91,7 m
(beim Abflugwinkel 45°), ein höchst unwahrscheinlicher Extremfall.
Stellen wir uns nunmehr vor, anstelle der Kugel hätten wir es mit einem Bruchstück
aus dem Zerplatzen eines Behälters zu tun. Dann wären neben Anfangsrichtung- und
Geschwindigkeit beispielsweise auch die Masse und Geometrie des Bruchstücks Zufallsvariable.
Hinzu käme, dass sich die Orientierung des Stückes während des Fluges änderte. Der
Luftwiderstand und eigentlich sogar seine Änderung infolge Lageänderung des Trümmerstücks
während des Fluges müssten berücksichtigt werden. Die Koeffizienten der entsprechenden
Differentialgleichung wären dann ebenfalls stochastischer Natur. Auch diese Fragestellung
ist probabilistisch. Sie wird z.B. in /4/, /5/ behandelt.
Fortsetzung
Deterministik und Probabilistik bei der Sicherheitsbeurteilung technischer
Anlagen
Es spricht also Einiges für die Aussage: “Das Verhalten von Naturphänomenen wird
durch den Zufall bestimmt und folgt nicht streng deterministischen Gesetzen“ /3/.
Dies gilt insbesondere im Bereich der Anlagensicherheit; denn der Zeitpunkt des Eintritts
eines Störfalls und das damit verbundene Schadensausmaß sind Zufallsvariable. Sie
können im Mittel, aber nicht im Detail, d.h. für einen konkreten Fall, vorhergesagt
werden.
Dies legt eine probabilistische Modellierung nahe. Sie ist umfassender als die herkömmliche
deterministische. Deshalb werden komplexere Modelle und somit auch mehr Eingangsdaten
benötigt als im deterministischen Fall. Es handelt sich also um eine Modellierung
auf einer höheren Ebene, die im Allgemeinen besser abgesicherte Ergebnisse und somit
auch verbesserte Entscheidungsgrundlagen liefert.
Allerdings wird die Qualität einer Analyse bestimmt durch die Qualität der Modellierung
und die Qualität der zugehörigen Eingangsdaten. Ein einfaches Modell mit wenigen
aber gut abgesicherten Eingangsdaten kann deshalb u. U. realistischere Ergebnisse
erzeugen als ein komplexes Modell, für das nicht ausreichend gute Eingangsdaten zur
Verfügung stehen. Was der bessere Weg ist, muss in Ansehung der jeweiligen Analyserandbedingungen
entschieden werden.
Bei dem vorangehenden Beispiel aus dem Bereich der Unfallfolgen geht es um stetige
Variable (Position, Geschwindigkeit etc.), deren Verlauf durch stochastische Differentialgleichungen
beschrieben wird. Mit solchen hat man es zum Beispiel auch in der Strukturmechanik
zu tun. Die Berücksichtigung des stochastischen Charakters, beispielsweise von Belastung
und Materialwiderstand, erlaubt es dort, die Versagenswahrscheinlichkeit von Strukturen
vorherzusagen /6/. Dabei kann es sich natürlich auch um passive Komponenten in Chemieanlagen,
beispielsweise Rohrleitungen und Behälter handeln. Die genannten Überlegungen haben
zum Gebiet der probabilistischen Strukturmechanik geführt. Aber auch im Bereich der
Störfallfolgenabschätzung /7/ oder bei der Auslegung von Anlagen werden stochastische
Gleichungen oder Differentialgleichungen zur Modellierung herangezogen /8/.
Eine Chemieanlage nutzt neben passiven Komponenten auch zahlreiche aktive Komponenten,
z.B. Regelventile. Deren Lebensdauern lassen sich derzeit nicht mit Hilfe von Differentialgleichungen
abschätzen. Stattdessen werden sie durch ein statistisches Modell beschrieben, das
in Abhängigkeit von der Zeit die Wahrscheinlichkeit für das Komponentenversagen angibt.
In probabilistischen Risiko- und Sicherheitsuntersuchungen werden die Komponenten
durch binäre Variable beschrieben, d.h. ihr Verhalten wird lediglich durch die zwei
Zustände „intakt“ oder „ausgefallen“ charakterisiert. Diese binären Variablen sind
unstetige stochastische Größen, sie nehmen also ihre beiden Zustände mit einer bestimmten
Wahrscheinlichkeit an, die vom betrachteten Zeitpunkt, aber auch beispielsweise von
der verwendeten Wartungsstrategie abhängt.
Bei der Ermittlung des Risikos technischer Anlagen geht es um die Abschätzung der
erwarteten Häufigkeit unerwünschter Ereignisse, beispielsweise der Freisetzung eines
toxischen Gases, und des mit diesem Ereignis verbundenen Schadensausmaßes (Störfallfolgenabschätzung).
Beispiel für eine probabilistische Risikountersuchung: Flughafen Frankfurt Landebahn
Nordwest
